Individuazione di anomalie nel consumo di energia elettrica
Ai giorni d’oggi, il consumo di energia elettrica è al centro dell’attenzione grazie al problema dell’ inquinamento globale.
Uno sforzo sempre più grande viene veicolato verso la risoluzione di questo problema. Per quel che concerne l’ Italia, essa si posiziona al 12° posto per consumo pro capite di energia elettrica:
https://en.wikipedia.org/wiki/List_of_countries_by_electricity_consumption
Con un consumo pari a 291 miliardi di kW*h/anno ed una meda di 4600 kW pro capite all’anno, l’Italia rimane uno dei principale paesi responsabili per l’eccesso di energia elettrica prodotta. In tale contesto, risulta interessante analizzare le dinamiche di comportamento dei consumi delle famiglie presenti sul territorio nazionale. In particolar modo l’interesse ricade nell’identificazione di comportamenti “anomali” durante un particolare giorno dell’anno. L’individuazione delle anomalie può risultare particolarmente utile per tutte quelle aziende coinvolte nella produzione di energia elettrica dal momento che essa non può essere immagazzinata una volta prodotta. Di converso, l’eccessiva richiesta di energia in uno specifico momento della giornata può anch’esso costituire un problema.
In questo articolo, viene proposta una combinazione di due particolari modelli per l’identificazione delle anomalie nei consumi di energia elettrica durante l’anno 2011. L’obiettivo dell’analisi, tuttavia, non è semplicemente quello di individuare consumi anomali ma di identificare irregolarità nella richiesta di energia elettrica durante la giornata (forma della distribuzione di energia elettrica).
L’articolo è strutturato nel seguente modo: in primo luogo, verrà fornita una breve descrizione riguardo al dataset preso in analisi ed il necessario pre-processing dello stesso al fine di poter assolvere al compito prefissato. A tal proposito, sarà proposta un’analisi grafica per comprendere appieno le connessioni esistenti tra le caratteristiche descrittive delle famiglie ed i consumi di energia elettrica. In secondo luogo, si effettuerà un’analisi più robusta dei dati tramite l’applicazione di una rete neurale non supervisionata (chiamata autoencoder) che consentirà di “codificare” la serie storica dei consumi delle famiglie. Fatto questo, sarà applicato un secondo algoritmo non supervisionato che prende il nome di Local Outlier Factor (LOF) (https://scikit-learn.org/stable/auto_examples/neighbors/plot_lof_outlier_detection.html) in grado di individuare anomalie rispetto all’andamento globale dei consumi elettrici (nota che un’altra possibilità è quella di utilizzare l’algoritmo pylof (https://github.com/damjankuznar/pylof)).
In ultimo, sarà fatta una ricapitolazione dei risultati ottenuti e sarà fornita una spiegazione dettagliata dei consumi anomali descrivendo le caratteristiche delle famiglie che risultano “differenti” rispetto all’andamento dei consumi complessivi di energia elettrica.
Creazione del dataset dei consumi elettrici
Al fine di poter applicare la riduzione di dimensionale tramite l’applicazione della rete neurale, abbiamo bisogno di modificare lo shape del nostro dataset. Il dataset di partenza si presenta con una forma pari a (35040; 377).
In altri termini, abbiamo 377 famiglie e per ognuna di esse una serie storica lunga un anno dove le osservazioni dei consumi sono rilevate ogni 15 minuti (35040 per ogni osservazione). In questo articolo, come detto in precedenza, l’interesse è quello di individuare anomalie nella forma in cui, durante un determinato giorno dell’anno, la richiesta di energia elettrica risulta sostanzialmente diversa rispetto a quanto mostrato dal vicinato (soggetti più simili all’osservazione in analisi). Per questo motivo, il dataset è stato modificato in modo tale da avere la seguente forma (137605, 96) dove ogni entry (osservazione) corrisponde ad un giorno dell’anno ed ogni colonna corrisponde ad un’osservazione del consumo di energia ogni quarto d’ora. In tal modo, ogni osservazione è ripetuta 365 volte dal momento che 96 quarti d’ora corrispondono alle 24 ore componenti l’intera giornata.
A parte le informazioni derivanti dal consumo di energie elettrica, abbiamo a disposizione anche un altro dataset in cui sono descritte le caratteristiche delle famiglie e le componenti dell’abitazione che maggiormente possono influenzare i consumi di energia elettrica. Alcune di queste variabili sono, il numero di elettrodomestici, il salario annuo, il numero di componenti della famiglia, e le zona climatica. Tale conoscenza, tuttavia, non sarà applicata all’individuazione delle anomalie ma sarà sfruttata per comprendere eventuali differenze tra comportamenti definiti outlier e non-outlier. In aggiunta alle osservazioni fornite, è stata effettuata una data augmentation in cui sono state aggiunte informazioni quali: giorni festivi, weekend e stagioni che possono in qualche modo descrivere e giustificare il perché una determinata osservazione è etichettata come outlier.
Analisi statistica descrittiva grafica
Come oramai usuale nei miei articoli, il primo passo è sempre quello di approcciare il problema tramite un’iniziale analisi descrittiva. In tal caso, tuttavia, s propone un’analisi grafica al fine di individuare eventuali legami interessanti tra le feature a disposizione.
Il primo passo è quello di realizzare una rappresentazione multipla dei consumi delle famiglie rispetto alla regione in cui risiedono. Per far ciò, sono stati sommati tutti i consumi di energia elettrica nelle 24 ore (ottenendo in questo modo l’intero consumo giornaliero di energia elettrica). Successivamente, è stata calcolata la media giornaliera dei consumi distinguendo su base annua e rispetto alle quattro stagioni dell’anno. L’immagine che segue, quindi, offre una interessante rappresentazione rispetto ai consumi di energia elettrica rispetto alla regione ed alla stagione dell’anno:
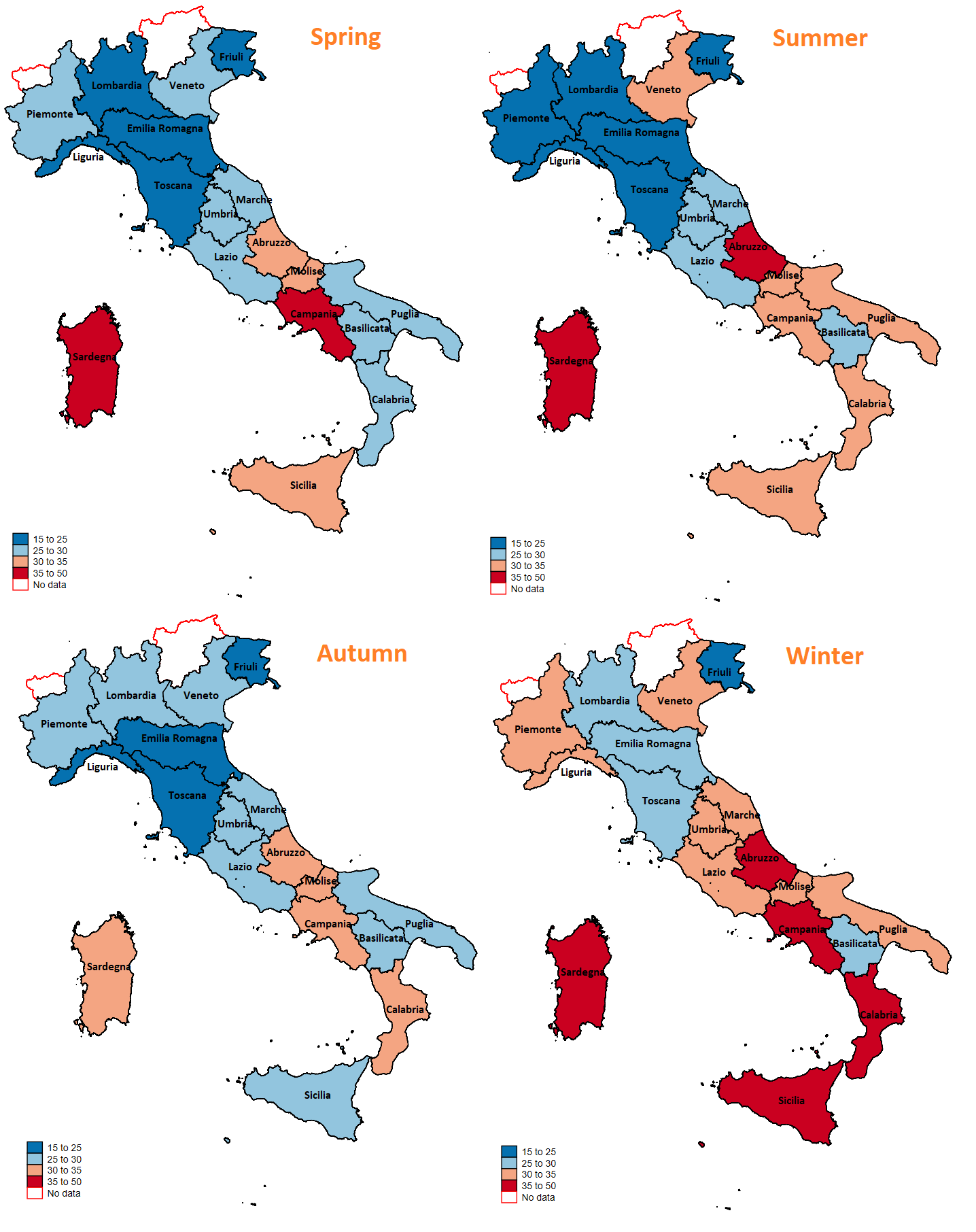
Dall’immagine sopra proposta, è possibile effettuare un’osservazione particolarmente interessante. Le regioni presente al nord, mostrano un consumo di energia meno pronunciato rispetto alle famiglie che risiedono al sud. Questo legame, inoltre, sembra essere robusto rispetto alla stagionalità e potrebbe essere dato dal fatto che le famiglie residenti al sud possiedono meno elettrodomestici “green” (a risparmio energetico). Tale affermazione, tuttavia, rimane una semplice speculazione dal momento che non si hanno a disposizione dati per avvalorare la tesi.
In aggiunta all’immagine proposta, si offre uno spaccato della numerosità campionaria delle 377 famiglie prese in considerazione per meglio comprendere quanto ogni regione è ben rappresentata in termini di numerosità campionaria:

L’istogramma mostra come la Lombardia sia la regione maggiormente rappresentata con un numero di osservazioni pari a 63. Di converso, il Friuli-Venezia-Giulia risulta la regione meno rappresenta con sole 3 osservazioni.
In ultimo, si mostra il box plot della distribuzione del consumo di energia elettrica delle famiglie per regione.
Tale analisi, tuttavia, mette in luce il consumo totale per l’intero anno 2011 di ogni famiglia in una specifica regione senza tener in considerazione la componente stagionale.
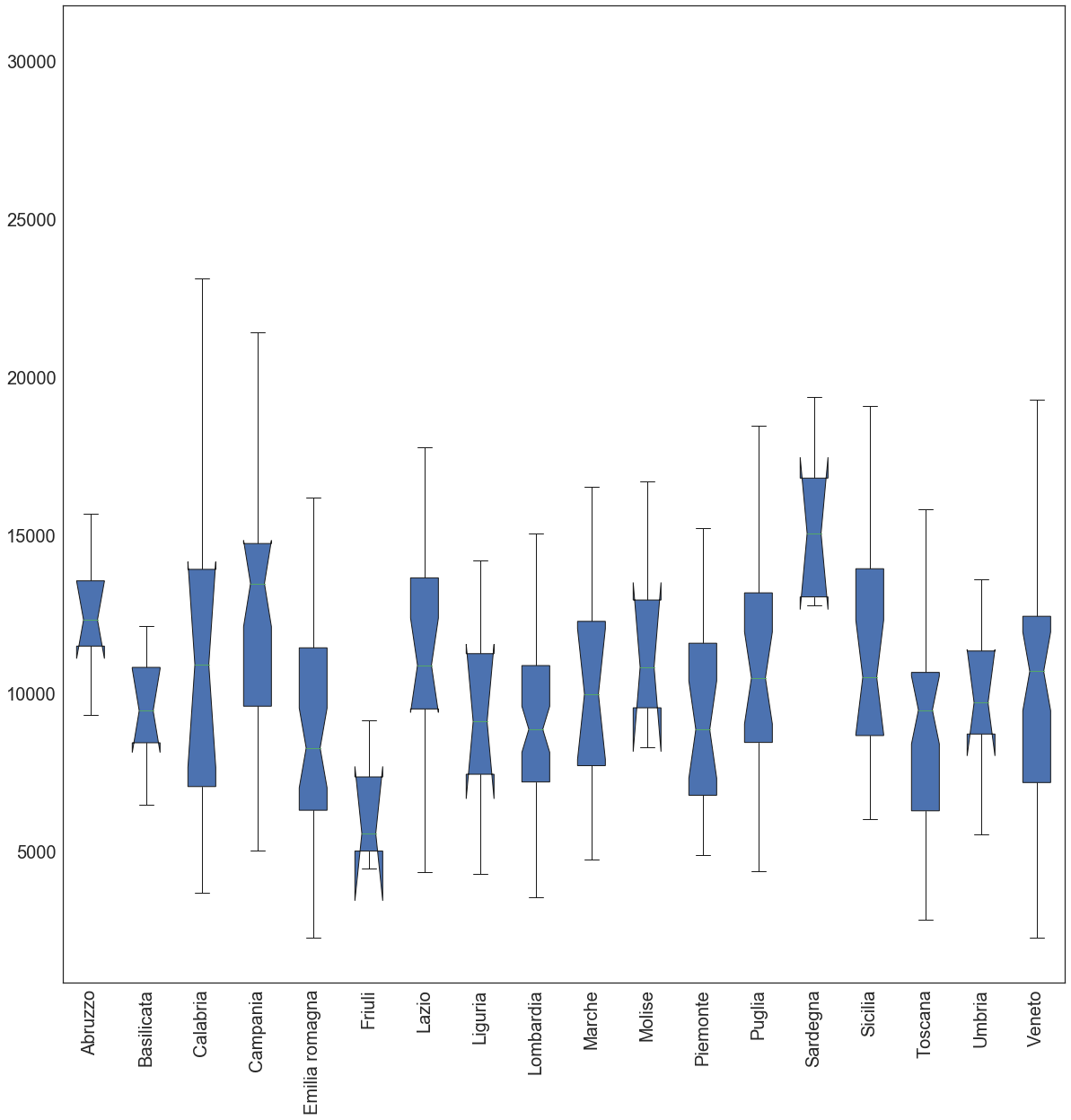
Dal grafico emerge che, coerentemente con quanto mostrato nella mappa tematica precedente, la regione Sardegna risulta senza dubbio la regione che il consumo di energia più elevato (valore mediano) e con una variabilità intraregionale contenuta. La regione Calabria, d’altro canto, riporta un consumo mediano di energia in linea con quello delle altre regioni del territorio italiano sebbene la variabilità intraregionale risulta particolarmente pronunciata. Per quel che concerne le informazioni descrittive delle famiglie e dell’abitazione in cui risiedono, si offre una rappresentazione concisa delle principali variabili ritenute più di rilievo (Numero di componenti famigliari, Salario annuo, zona climatica e approvvigionamento energetico [kW]):
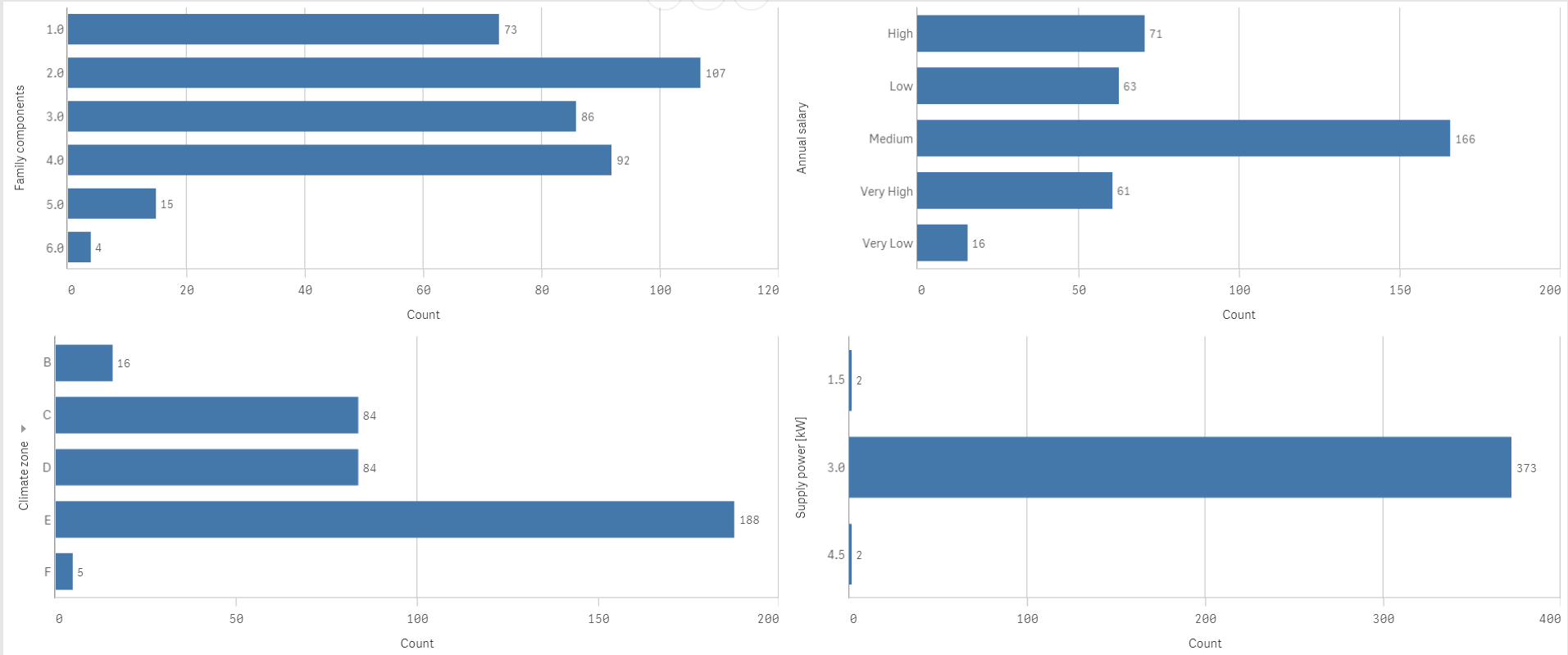
Il grafico a barre mostrato in alto, mostra come l’approvvigionamento di energia elettrica è praticamente identico per tutte le famiglie in analisi (grafico in basso a destra) con un livello pari a 3 kW. In aggiunta, il nostro dataset è costituito principalmente da coppie (107 su 377) ed un livello medio di salario (166 su 377).
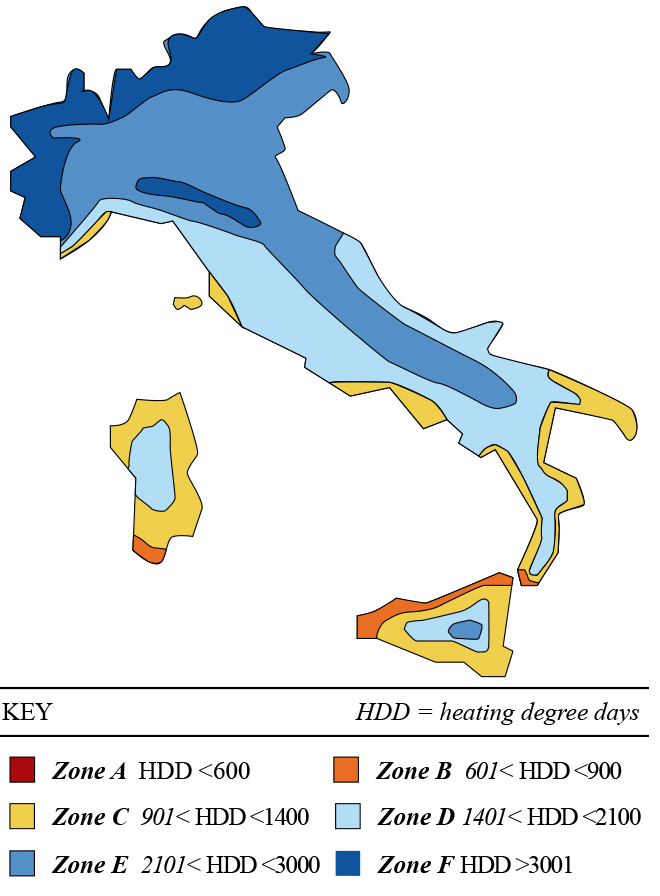
In ultimo, per quel che concerne la zona climatica, l’Italia è classificata essenzialmente come zona E e dove tale classificazione viene definita sulla base del grado giorno:
”Heating degree day” (HDD) è una misura che ha come obiettivo quello di definire il consumo di energia elettrica necessaria per riscaldare un palazzo. L’HDD è ottenuta prendendo in considerazione le misurazioni di temperatura dell’aria. Il calore necessario per il riscaldamento di un palazzo in una determinata località, è direttamente proporzionale che io valore di HDD in quella determinata zona. Una misura simile (CDD – cooling degree day) riflette l’ammontare di energia necessaria per raffreddare un’abitazione;
L’immagine seguente rappresenta la distribuzione della misurazione di HDD sul territorio:
In ultimo, vengono proposto quattro grafici combinati (joint plot) per le variabili seguenti:
superficie della casa (metri quadrati) salario annuo, numero complessivo di elettrodomestici rispetto al consumo di energia elettrica. In basso a destra, invece si mostra la correlazione tra il numero di elettrodomestici e la superficie della casa:
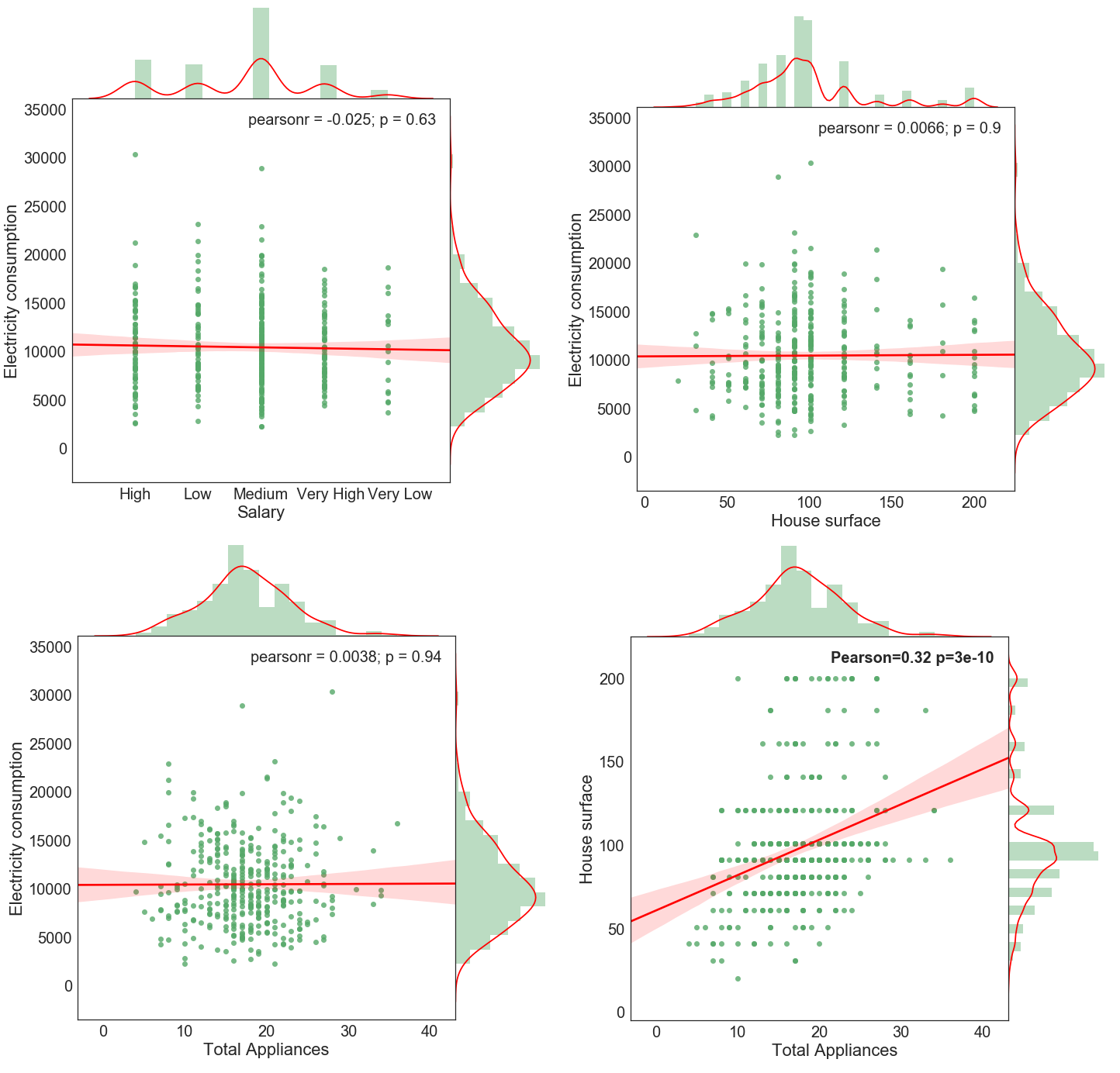
Il joint plots proposto è composto da uno scatterplot in cui si mostra la relazione tra le due variabile in analisi, mentre all’esterno si riportano le distribuzioni univariate delle singole variabili. Nell’angolo in alto a destra, inoltre, si riporta il coefficiente di correlazione di Pearson seguito dal corrispondente p-value. Ad esclusione del grafico in basso a destra, non è presente alcuna correlazione lineare tra le variabili in analisi in cui il p-value riportato è ben al disopra gli usuali intervalli di confidenza.
Al fine di soddisfare la curiosità, si propone la correlazione tra il numero totale di di applicativi e la superficie dell’abitazione. Come ci si aspetta, è presente una consistente relazione positiva tra le due variabili con un coefficiente di Pearson pari a 0.32 che risulta essere statisticamente significativo.
Analisi profonda delle anomalie
Dopo aver esplorato interamente il dataset a nostra disposizione, si propone un’analisi più avanzata il cui obiettivo è quello di individuare andamenti anomali nella richiesta di energia elettrica. Per assolvere al task si propone una rete neurale in gradi di codificare i consumi di energia elettrica durante la giornata (le 96 osservazioni rilevate ogni 15 minuti) riducendone la dimensionalità a 3.
Per far ciò, è stata applicata la seguente struttura di rete neurale:
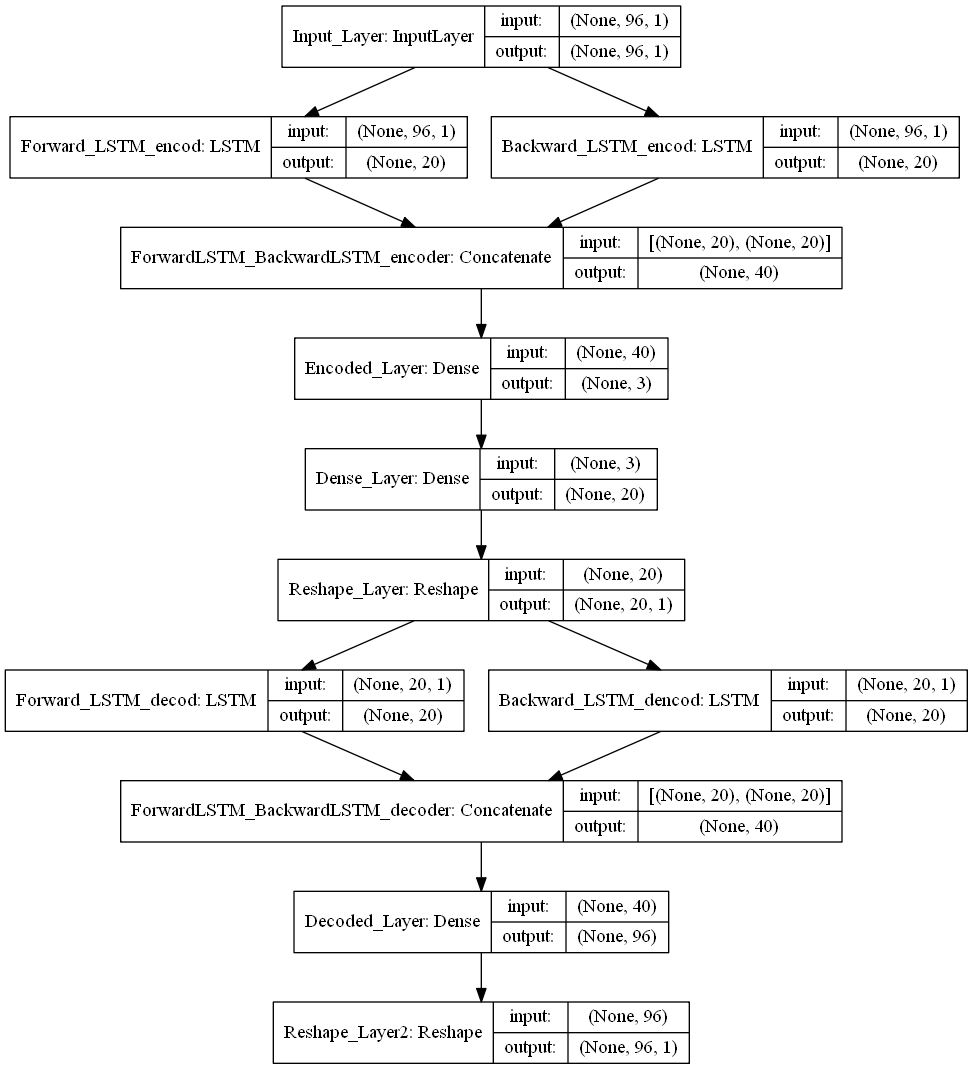
La rappresentazione della rete neurale mostrata qui sopra, non rappresenta l’output offerto da Keras. Tale immagine tuttavia, può essere facilmente ottenuta grazie al package chiamato: ‘Graphviz’ (https://graphviz.gitlab.io/download/).
Dall’immagine, è possibile cogliere come il problema di riduzione di dimensionali, nel nostro caso, ricade nella categoria dei problemi di regressione. I dati di origine sono letti dalla rete tramite il layer di input (Input_Layer) e codificati in uno spazio a 3 dimensioni grazie al layer di codifica (Encoded_Layer). L’output di questo layer è ciò che utilizzeremo per individuare le anomalie. Tuttavia, al fine di poter codificare correttamente i dati in ingresso, la rete neurale dovrebbe essere in grado, partendo dai soli dati codificati, di ricostruire il vettore in input (di 96 dimensioni). Questo è, in effetti un compito particolarmente ardue che la rete, tuttavia, è in grado di assolvere. Le performance del modello sono quindi valutate rispetto alla capacità di ricostruire il vettore di origine e l’errore è calcolato come RMSE rispetto ai dati in input che rappresentato la groud truth.
Il seguente grafico mostra le performance del nostro modello comparando la “training loss” rispetto alla “validation loss”:
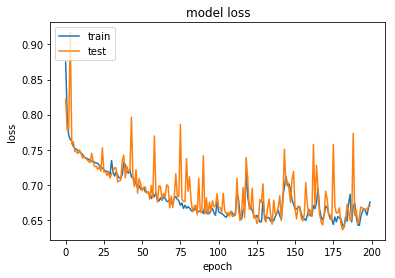
A parte le poco interessanti fluttuazioni ottenute dalla validation loss (dovute ad una bach size abbastanza piccola), il modello proposto sembra approssimare bene i dati ed ambedue le funzioni di perdita si riducono monotonicamente raggiungendo un RMSE pari a 0.74 nel gruppo di validazione.
In questa sede, tuttavia, si vuol far notare come una bach size particolarmente ristretta possa portare ad una maggiore accuratezza del gradiente, nel senso che quest’ultimo possa essere più vicino rispetto al “vero” gradiente ottenibile se si processasse ogni volta l’intero dataset (whole-batch). Come noto, tuttavia, esiste un trad-off rispetto alle performance inerenti la selezione della batch size. Una grande batch size è solitamente considerata computazionalmente più efficiente (fino ad un certo punto), ma sebbene tale processo possa incrementare il numero di campioni processati (e quindi ne segue un diretto incremento del tempi necessario per completare ogni epoch) può anche voler dire un minor numero di iterazioni necessarie all’algoritmo SGD (Stochastic Gradient Descent) per convergere.
I più recenti studi, a tal riguardo hanno mostrato come sia preferibile, specialmente con reti neurali profonde, considerare batch size più piccole rispetto a processare l’intero dataset ogni volta.
Una volta codificato il dataset di interesse, si procede nell’applicazione dell’algoritmo LOF in grado di individuare outlier definiti, in questo caso, come l’1% dei valori più estremi rispetto al vicinato che lo compone. La dimensione del vicinato è un parametro di tuning che nel nostro caso è stato fissato pari a 570. Si noti che, tale parametro risulta particolarmente importante nella definizione di cos’è un outlier dal momento che un’osservazione può ricadere o meno in tale definizione a seconda del vicinato con cui è messo a confronto. L’immagine seguente riporta una rappresentazione dinamica in 3D rappresentate un campione di numerosità 1000 estratto random dall’intero dataset codificato nel passaggio precedente:
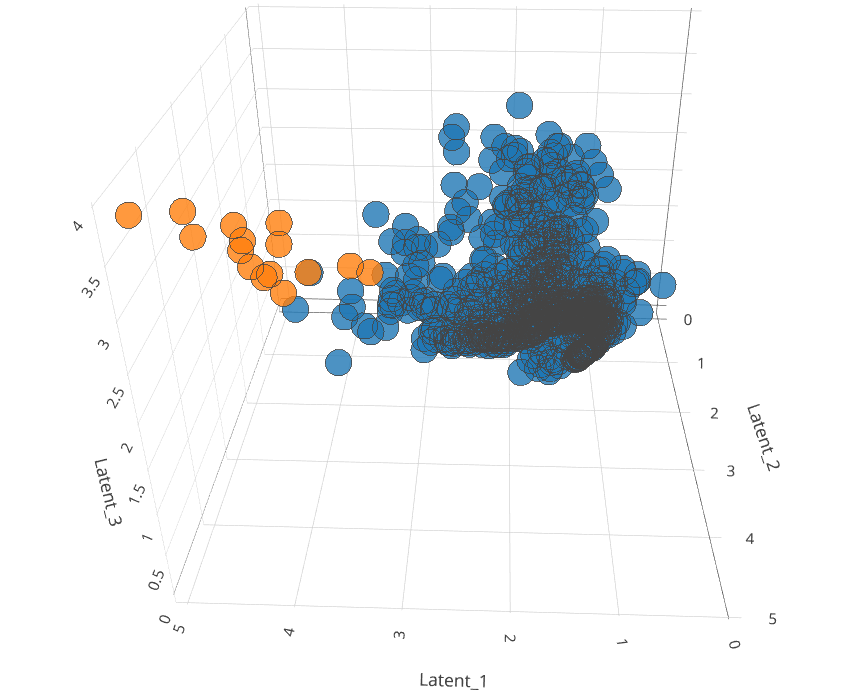
Dal grafico è possibile notare come il modello LOF sia particolarmente “bravo” ad individuare osservazioni al margine della distribuzione (pinti arancioni). Ricordiamo che il proposito nell’usare una combinazione di modelli non supervisionati per l’individuazione di comportamenti anomali tra le famiglie del campione sta nel fatto che il primo (autoencoder) codifica i dati in uno spazio dimensionale ridotto rispetto a quello di partenza. Il secondo, consente, prendendo in considerazione il campione codificato, di individuare le osservazioni al margine.
La codifica dei dati in uno spazio dimensionale ridotto risulta utile per due principali motivazioni. La prima deriva dal fatto che il concetto di vicinanza in un spazio dimensionale aumentato risulta particolarmente onerosa data la scarsità dei dati (course of dimensionality).
La seconda motivazione deriva dal fatto che al fine di poter settare correttamente i parametri del modello di LOF (specialmente la dimensionalità del vicinato) è necessaria un’analisi grafica in grado di dare un riscontro visivo sulla reale identificazioni delle osservazioni anomale. Questo problema è ciò che usualmente si riscontra con l’utilizzo di algoritmi non supervisionati in cui non si ha alcun riscontro riguardo la bontà di adattamento del modello hai dati. Effettuando l’analisi completa all’intero dataset, siamo in grado di monitorare i giorni in cui è presente un comportamento anomalo da parte di una famiglia durante l’arco della giornata.
Inoltre, siamo in grado di descrivere le caratteristiche della famiglia nonché dell’abitazione in cui vive:
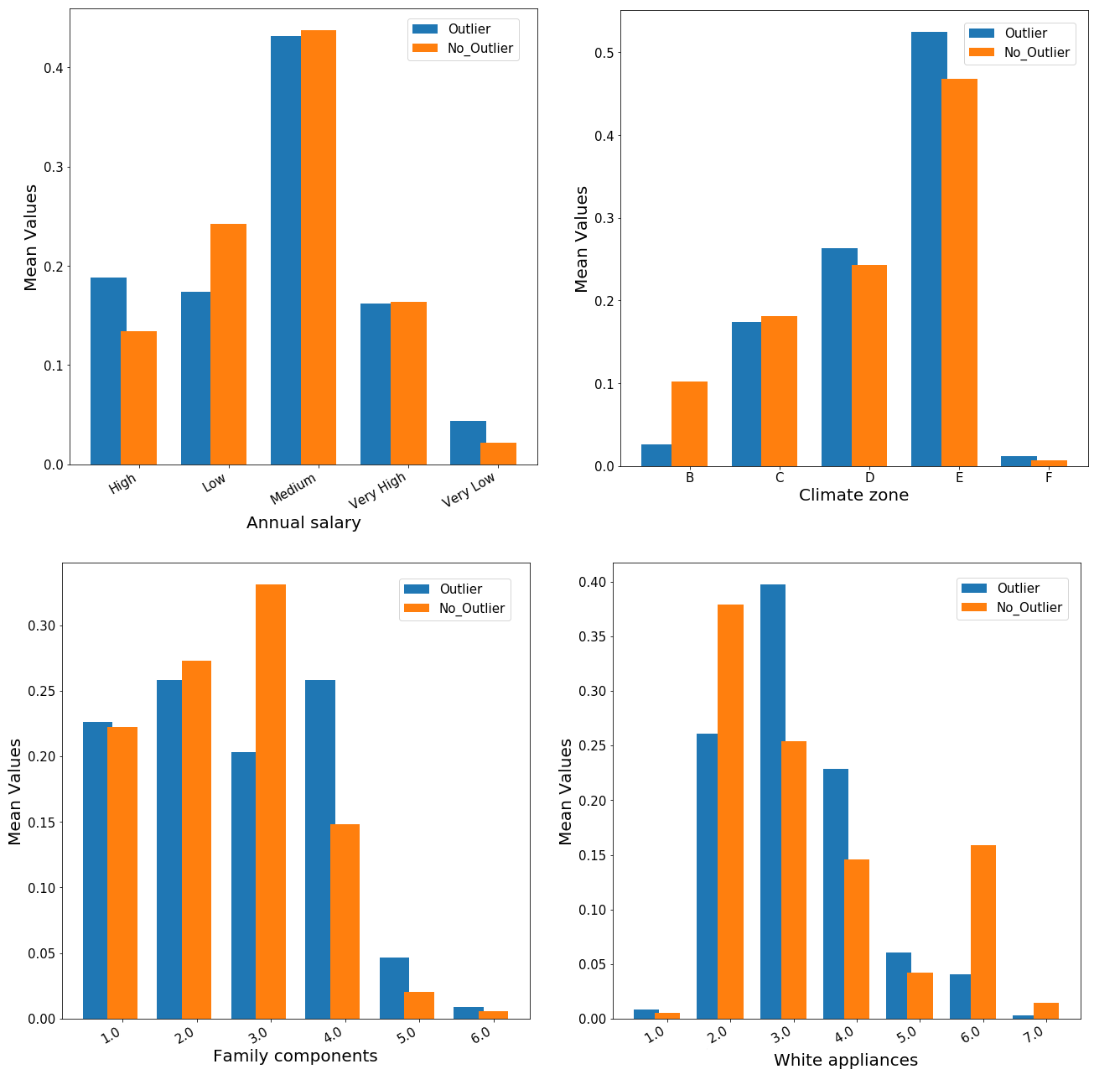
Dai risultati mostrati nei grafici a barre sopra riportati, non è presente alcuna differenza statisticamente significativa tra i due gruppo (outlier vs non-outlier). Tele risultato piò essere deviato dal fatto che, la numerosità campionaria delle famiglie in analisi risulta particolarmente bassa (377 osservazioni) ed i parametri della rete neurale non sono stati appositamente settati dato il time constraint posto. Ad ogni modo, è possibile comunque trarre alcune interessante informazioni dall’analisi sopra riportata semplicemente confrontando i due gruppo per ciascuna classi di ogni variabile. In primo luogo, sebbene non troppo pronunciato, il gruppo “anomalo” mostra una prevalenza di soggetti con alto salario ma anche con salario molto basso. Per quel che concerne la zona climatica, una visibile differenza può essere riscontrata per le classi B ed E. Inoltre, per le famiglie outlier si ha un numero di elettrodomestici mediamente pari a 4 mentre per gli elettrodomestici bianchi, sembra esserci una prevalenza rispetto nel possedere da 3 a 4 componenti rispetto ad una media di 2 o 6 per i soggetti non-outlier.
La stessa analisi è stata effettuata rispetto alle variabili temporali:
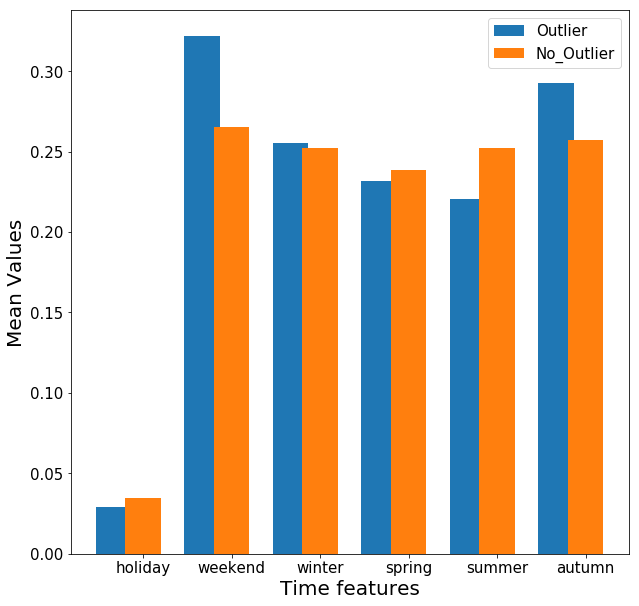
Dal grafico sopra riportato, è possibile notare che il gruppo outlier è più presente nel fine settimana ad in autunno sebbene tali differenze risultano minime.
Conclusioni
In questo articolo abbiamo analizzato il consumo elettrico di 377 famiglie sparse sul territorio nazionale per l’intero anno 2011. L’obiettivo dell’analisi è stato quello di individuare anomalie nel consumo di energia elettrica in uno specifico giorno dell’anno. Al fine di poter assolvere all’oneroso compito, si è proposta una combinazione di due modelli di machine learning non supervisionati.
Nella prima parte dell’articolo, si sono mostrate alcune statistiche descrittive, in via grafica, dove è stata effettuata un’esplorazione del dataset e delle possibili relazioni tra variabili. Da qui si è notato come il consumo di energia elettrica sia legato alla stagionalità e del livello di sviluppo regionale in cui la famiglia risiede, dal momento che le regioni del nord Italia sono notoriamente quelle economicamente più sviluppate. Nella seconda parte dell’articolo, invece, si è proposta un’analisi più sofisticata in cui il primo passo è stato quello di ridurre il vettore di input, composto da 96 osservazioni ogni 15 minuti, in uno spazio dimensionale ridotto (3 dimensioni).
Il dataset così codificato è stato utilizzato per individuare le osservazioni al margine della distribuzione e per essi sono state effettuate le usuali statistiche descrittive spetto alle caratteristiche delle famigli e dell’abitazione in cui risiedono. A parte differenze di poco conto, non si riscontrano differenze sostanziali tra i due gruppo a livello statisticamente significativo.
info su: https://medium.com/yadb/electricity-consumption-outlier-detection-4904cb196a2c