Scoperta di pattern sconosciuti nelle reti social
La scoperta di pattern sconosciuti all’interno di dati è un compito complesso che necessita di tecniche algoritmiche spesso complesse e che possono variare in base alla tipologia di dati che si vogliono analizzare. In questo articolo, descriveremo l’applicazione di una particolare tecnica di machine learning non supervisionato nota come Fattorizzazione Tensoriale Non Negativa al problema della scoperta di pattern sconosciuti all’interno di reti sociali che cambiano nel tempo.
Il presente articolo è diviso in due parti. Nella prima parte, forniremo una breve introduzione alla fattorizzazione tensoriale non negativa. Nella seconda, applicheremo concretamente, utilizzando Python, tali algoritmi a dati reali.
Fattorizzazione tensoriale
Iniziamo dando una breve introduzione al concetto di tensori e di fattorizzazione tensoriale. All’interno di questo articolo faremo diversi riferimenti ad alcune definizioni fornite in Kolda et. al, Tensor Decompositions and Applications, SIAM Review, 2009, Vol. 51(3): pp. 455–500. (https://epubs.siam.org/doi/abs/10.1137/07070111X?journalCode=siread)
Un tensore è un array multidimensionale. Un tensore di primo ordine è un vettore, un tensore di secondo ordine è una matrice, tensori di terzo (Figura 1) o ordine maggiore invece sono chiamati vettori di alto ordine. (Kolda et. al, Tensor Decompositions and Applications).
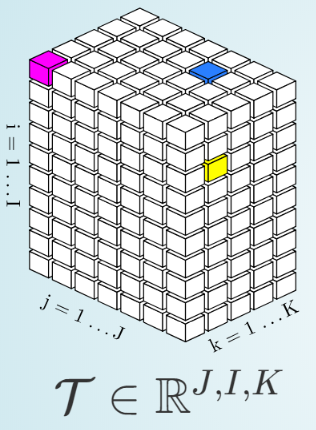
Figura 1 Struttura di un tensore
Scopo della fattorizzazione tensoriale è quella di ottenere una rappresentazione compatta dei dati contenuti nel tensore. Una delle procedure più note per effettuare la fattorizzazione tensoriale è la canonical polyadic decomposition (CPD). Questo tipo di decomposizione fattorizza un tensore nella somma di componenti ciascuno dei quali è un tensore di rank uno (Figura 2).

Figura 2 Non-Negative Canonical Polyadic Decomposition (NCPD) per la fattorizzazione tensoriale
In Figura 2, abbiamo graficamente introdotto un particolare tipo di CPD nota come Non-negative CPD (NCDP). La differenza con la classica CPD risiede nell’imposizione del vincolo di non negatività dei fattori. Uno dei parametri più importanti della fattorizzazione tensoriale è la scelta del Rank (R). Più formalmente:Il rank (R) di un tensore T denotato con rank(T), è definito con il più piccolo numero di componenti di rank 1 che generano T. (Kolda et. al, Tensor Decompositions and Applications)Sfortunatamente la scelta del rank ottimale è un task complesso che deve essere guidato dalla conoscenza che si ha dai dati.
Estrazione di pattern da reti sociali in Python
Qui di seguito mostriamo come utilizzare la fattorizzazione tensoriale in Python per l’estrazione di pattern sconosciuti. I dati usati in questo articolo sono stati selezionati dal sito Index of Complex Network (https://icon.colorado.edu/#!/networks). Nello specifico, abbiamo selezionato il dataset Golden Age of Hollywood. Il dataset consiste nelle collaborazioni di 55 attori molto proficui durante l’“età d’oro di Hollywood” (1930-1945). I nodi di tale rete sono gli attori, mentre gli archi che li collegano, identificano se due attori sono stati nello stesso film.
I grafi del dataset sono stati trasformati nelle rispettive matrici di adiacenza. Tali matrici sono dunque state concatenate nella terza dimensione al fine di generare una matrice a 3 dimensioni (Figura 3).

Figura 3 Creazione di un tensore a partire dalle matrici dei grafi
Il caricamento dei dati e la loro strutturazione sono eseguiti tramite il seguente codice Python (Figura 4).

Figura 4 Caricamento del dataset
Prima di concatenare le matrici provvediamo a rimuovere gli auto-archi mettendo zero nella diagonale delle matrici.
Possiamo ora effettuare la fattorizzazione utilizzando Python. Un ottimo tool è Tensorly (http://tensorly.org/stable/modules/api.html#module-tensorly.base). Tale libreria infatti contiene una vasta gamma di funzioni utili per poter trattare in modo semplice i tensori.
Il primo passo di tale processo è quello di trasformare i nostri dati in un tensori nel formato utile a Tensorly per poter lavorare (Figura 5).

Figura 5 Conversione dei dati in formato tensorly
Possiamo adesso effettuare la fattorizzazione. Per questo esempio abbiamo scelto di estrarre 20 componenti (Figura 6).

Figura 6 Codice per eseguire la fattorizzazione non negativa
Il risultato della fattorizzazione è memorizzato nell’array “factors”. Eseguiremo dunque un’analisi esplorativa per verificare quali pattern sono stati identificati nei diversi componenti. In questo articolo eseguiremo solo l’analisi di alcune sorgenti.
Al fine di rendere più semplice ed intuitiva l’esplorazione dei diversi pattern contenuti all’interno delle diverse sorgenti, utilizzeremo delle rappresentazioni grafiche. A tal fine, due librerie sono state utilizzate: matplotlib (https://matplotlib.org/) e NetworkX (https://networkx.github.io/).
Per ciascuna componente, due diverse informazioni vengono analizzate: 1) Il prodotto tra i fattori A e B. 2) I valori del fattore C. L’idea principale di questi plot è quella di mostrare rispettivamente 1) quali pattern sono stati estratti dalla componente e 2) quali sono gli istanti temporali nei quali tali pattern sono presenti. Il codice utilizzato per effettuare tali plot è disponibile in Figura 7.
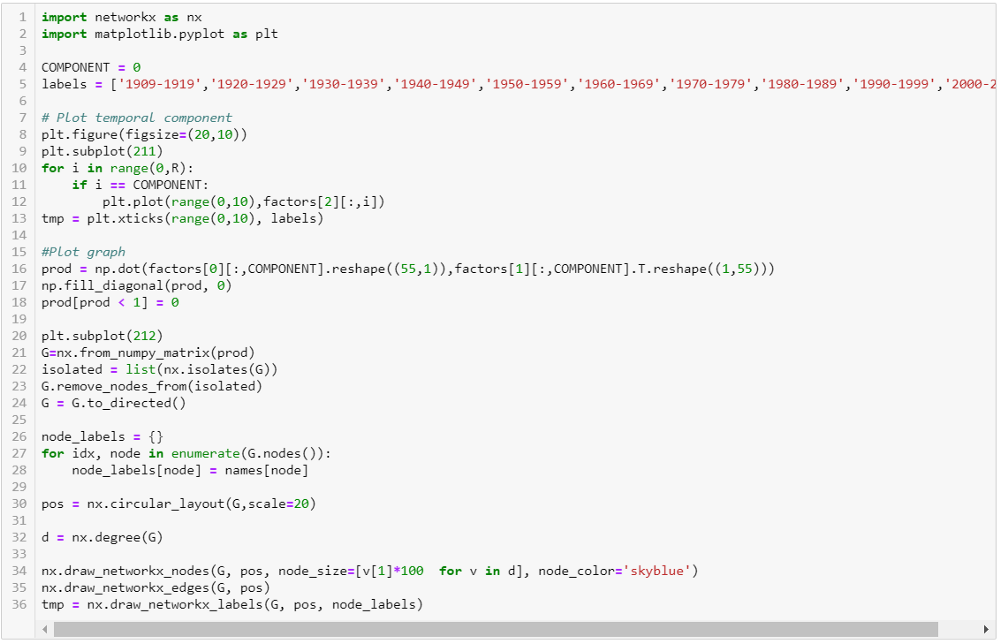
Figura 7 Codice per plottare i diversi valori di una data componente
Qui di seguito uno dei plot che è possibile ottenuti da questo processo:

Figura 8 Informazioni ottenute dalla componente #0. Sopra. Il plot del fattore C. Sotto. Il pattern spaziale ottenuto da A e B
Cerchiamo ora di capire il significato di questi plot. Il pattern contenuto dalla componente #0 può essere identificabile con la filmografia dei fratelli Marx. Infatti, se ci focalizziamo sulla parte inferiore di Figura 8, possiamo notare un network nel quali i fratelli Marx sono strettamente collegati tra di loro. Una altra informazione di notevole interesse è anche presente nella parte superiore di Figura 8. Infatti, il pattern temporale ricalca esattamente il numero di film per anno nei quali i fratelli Marx sono presenti. Se analizziamo i dati sulla loro filmografia disponibili su wikipedia (Figura 9) possiamo vedere come l’overlap di questa con la componente C sia perfetto. Infatti, per un totale di 17 film in comune. 2 (11.8%) sono stati girati tra il 1920-1929, 9 (52.9%) nel 1930-1939, 4 (23.5%) nel 1940-1949 e 2 (11.8%) nel 1950-1959.
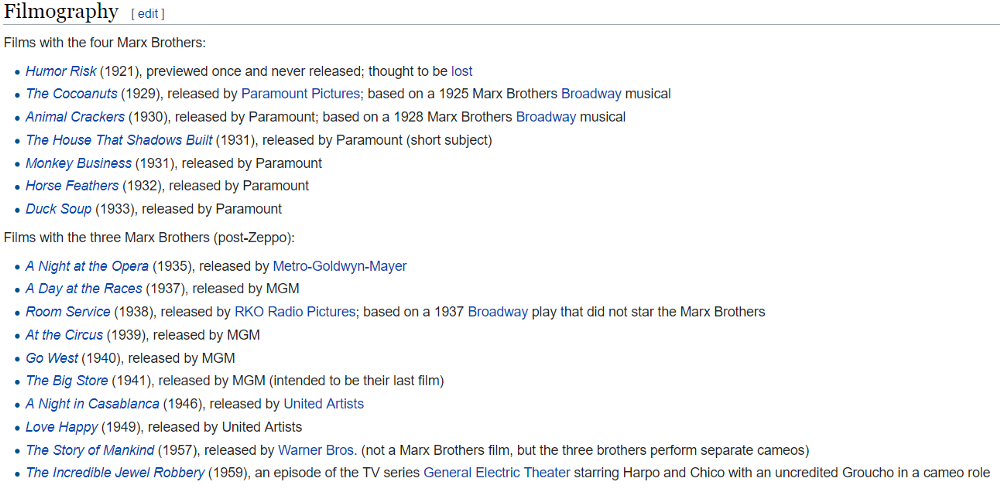
Figura 9 La filmografia dei fratelli Marx estratta da Wikipedia
Un’altra componente che contiene informazioni interessanti è la #4 come mostrato nella seguente immagine.
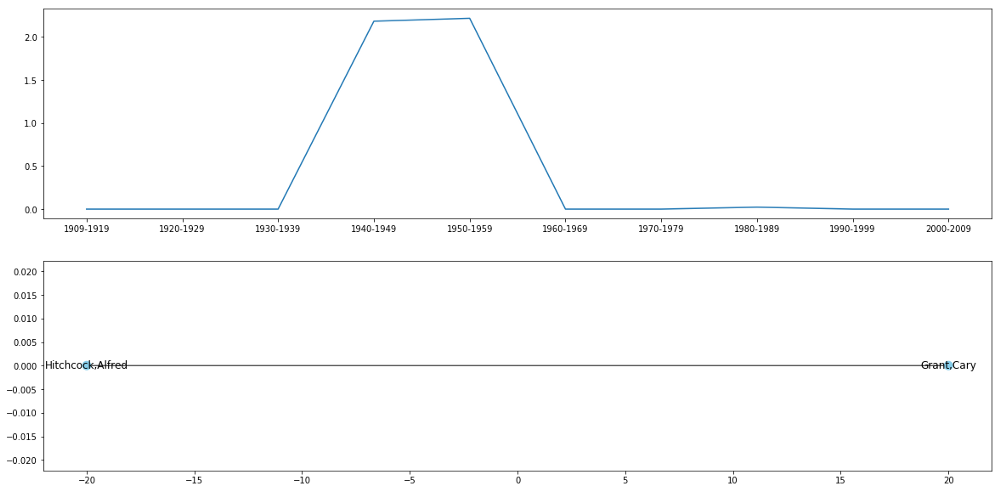
Figura 10 Informazioni estratti dalla componente #4. Sopra. Plot del fattore C. Sotto. Grafo ottenuto da A e B
Nel dettaglio, questa componente rappresenta uno delle più collaborazioni più celebrate tra Attore e Regista, quella tra Alfred Hitchcock e Cary Grant, visibile nella parte inferiore della Figura 10. Se vediamo la parte superiore, possiamo notare due picchi nel range 1940-1949 e 1950-1959. Questo risultato ricalca i 4 film girati. 2 nel 1940-1949 (“Suspicion” — 1941 e “Notorious” — 1949) e 2 nel 1950-1959 (“To Catch a Thief” — 1941 and “North by Northwest” — 1949).
Conclusioni
In questo articolo abbiamo mostrato un semplice metodo per poter identificare pattern sconosciuti all’interno di network che cambiano nel tempo. Più nel dettaglio, nella prima parte, abbiamo dato alcuni cenni sui tensori e sulla fattorizzazione non tensoriale. Abbiamo in seguito applicato tali algoritmi ad un dataset pubblicamente disponibile in rete. Python è stato dunque utilizzato per poter effettuare la fattorizzazione e dati e la relativa rappresentazione. Il risultato più interessante ottenuto da tale processo è quello relativo all’identificazione di pattern non visibili nei dati. Da tali pattern infatti siamo riusciti ad estrarre informazioni non chiaramente visibili dalla mole di dati iniziale.